Hairetdinov
R. F.
THE SOLUTION OF THE CUBIC EQUATIONS.
2005
year
Introduction.
The studying of the solution of the cubic equations usually concerns to
a course of the higher algebra and connects with the theory of functions of the
complex variable (TFCV). Thus formula Cardano is used which is applicable only
in special cases at the certain correlations of factors of the cubic equation.
In other cases final formulas for calculation of roots of the cubic equations
are difficult and accessible only after studying TFCV.
In this article the way of the solution of the cubic equations is
expounded with the help of quickly converging recurrent formulas which are
received by using of the universal cubic equations. Thus there is no necessity
of studying TFCV and it is enough to acquire knowledge in the field of
mathematics received in the secondary school.
These
offered recurrent formulas for the solution of the cubic equations are rather
easy and allow to get solutions with accuracy and for a short period of time. Thus
we can use both usual pocket scientific calculators, and programmable, that is
especially convenient for using of recurrent formulas.
The studying and the development of this offered way of the solution of
the cubic equations allow to master the bases of the solution of the degree equations, to receive skills of using
of recurrent formulas and programming at calculation with the help of recurrent
formulas even at a secondary school.
1.
The
using of formula Cardano
The
cubic equation in a general view is known (L1)
![]() (1)
(1)
that
it is possible to transform to the reduced kind
![]() (2)
(2)
having
substituted in (1) instead of õ expression
![]() (3)
(3)
For all that
![]() (4)
(4)
![]() (5)
(5)
The cubic equation of kind (2) we name the reduced
cubic equation (for brevity: RCE).
Further for the simplification of writing of formulas
RCE we drop an index «y» at factors Ây and
Dy, and
the formula RCE we write down as
![]() (6)
(6)
At the certain (mentioned below) correlation between
factors B and D the value of a material root
y1 RCE can be calculated with the help of
formula Cardano that is below in the modified kind:
 (7)
(7)
where
![]() - factor RCE.
(8)
- factor RCE.
(8)
From
the formula (7) it is clear, that for the receipt of material numbers under the
sign of a square root there should be a number, the greater or equal to zero,
i.e.
![]()
In cases when ty > 6,75, under the formula (7) the imaginary
(complex) numbers turn out, and for the receipt of values of roots RCE as
material numbers it is necessary to use the theory of functions of complex
variable ( TFCV) (L1).
In section 3 and further the way of solution RCE is
offered which is different from the way of Cardano and it does not demand the
using of TFCV for calculation of material values of roots RCE at any sizes of a
factor ty.
2. The calculation of the second and
third roots of the cubic equation.
For the
explanation of some moments we consider RCE with the concrete numerical data:
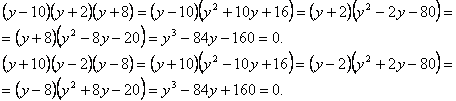
The
equations above have 3 various material roots and in the quality y1 (the first root) choose that root,
which has a maximal (on the module) size, and in the quality y2 and y3
are the other two roots of the same sign.
 (1)
(1)
In the examples with the numerical data y1 = + 10 and 10;
y2 = 2 and +
2;
y3 = 8 and +
8, d = + 16.
The
size d (equal to the product y2 ∙ y3 with identical signs) always has a sign «+». The
signs y1 and D are
always different. There are examples of RCE below with one material root and
two imaginary roots.

In
the examples above y1 = +10 and 10 are material roots, y2 and y3
are the imaginary roots which are turning out after the solution of
quadratic equations of decomposition RCE.
The
quadratic equation of the decomposition (1) looks like
![]() .
(2)
.
(2)
The
formula (2) can be used at calculation of sizes of roots y2 and y3
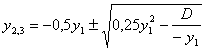 (3)
(3)
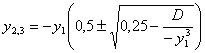 (4)
(4)
When ty
< 6,75 and y2,3 are imaginary roots,
also there is no necessity to calculate numerical parameters of imaginary roots
then the decomposition (1) can be presented as the solution RCE, and it is
possible to check of correctness of solution
RCE by checking the equality received
from formulas of the decomposition (1):
![]() (5)
(5)
Note1.
At the reference to formulas of the other unit we designate them as (N K), where N is a number of the section, K
is a number of the formula in this section.
Note2.
After the definition of roots RCE the calculation of roots of the initial
solved equation (1 1) is under the formula (1 3)
![]() .
.
3. The universal cubic equation of kind
1.
Let ![]() (1)
(1)
After
the substitution (1) in the formula (1 6) and the transformations we receive:
![]() (2)
(2)
where ![]() (3)
(3)
The formula (2) we name it as the formula of the
universal cubic equation of
a kind 1 (for brevity further UCE 1).
Under the formula (3) the factor RCE is calculated at
the solution by UCE 1. Under the formula (1) the first root RCE on the size
"k" (the first root UCE
1) and the size of the factor D in
the formula (1 6) is calculated. We take the size k in formulas (1) and (2) from zero up to (+ ∞), i.e. k ≥ 0.
The
size ky in
formulas (2) and (3) can accept the value from (-∞) up to (+ ∞).
The
universality of the formula (2) is that any cubic equation of a kind (1 1)
can be reduced unequivocally to the formula (2), the solution of the equation
(2) depends only on one parameter the factor ky, the dependences ky
= f(k) è
k = φ(ky) under the condition of k > 0 are
unequivocal at any sizes ky (îò ∞ äî
+ ∞).
The cubic function under the formula (2) can be
represented at k > 0 as the graph ky = f (k) or to present as
the detailed tables.
The algorithm of solution RCE through UCE 1 consists
of the calculation of the parameter ky under the formula (3), the definition the of size «k» on the size
of the parameter (factor) ky with the formula (2) and the calculation of the size
of the first root y1 RCE under the formula (1). For the solution UCE 1, except the graph
ky = f (k) or tables, it
is possible to use the formulas received further according the text. In this
article the recurrent formulas are used on which calculations are conducted by
a method of iteration cyclically before the reception of the result with
necessary exactness. In each new iteration, the result of the previous
iteration is used.
The recurrent formula is suitable for using if the
mistake of result, after each iteration decreases, it means, that the recurrent
formula possesses convergence.
As a rule, the recurrent formulas possess convergence
not at all possible values of a parameter (the factor of the cubic equation),
but only in some working area of a parameter with concrete borders for each
recurrent formula.
Also the recurrent formulas differ from each other in
the speed of convergence, i.e. in the size of the ratio of the module of a
results mistake received in the previous iteration, to the module of a
results mistake received in the subsequent iteration.
If the speed of convergence is more than a unit the
formula has convergence at the given value of a parameter.
From some set of the recurrent formulas which can be
received from the formula (2), the following have been selected on the speed of
convergence:
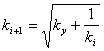 (4)
(4)
![]() (5)
(5)
The method of the calculation of the speed of
convergence of the recurrent formulas we show by the example of the formula (4).
At k =
2 under the formula (2) ky = 3,5 .
Let
suppose that the result of the previous calculation was ki = 1,99 with a mistake (on the module) |∆1|
= k ki = 2 1,99 = 0,01 .
Under the formula (4) we receive the size ki+1 = k2
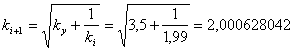
The module of a mistake of the result, received after (i + 1) cycle of calculations is |∆2|
= 2,000628042 2,0 = 0,000628042 .
The speed of convergence in the set conditions is
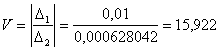
Let's calculate the speeds of the convergence which
are turning out at a variation of set conditions.
Let k1
= 2,01, |∆1| = 2,01 2,0 = 0,01
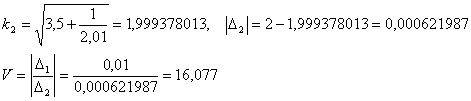
Let k1 = 3,0, |∆1| = 3 2 =
1

Let k1 = 1,0, |∆1| = 2 1 =
1

From the comparison of results of calculations it is
possible to conclude, that the speed of a convergence depends on the size and
the sign of a mistake of the initial value of the unknown quantity, and for the
comparison of various formulas on the speed of convergence it is necessary to
set identical initial conditions (an identical sign and the size of a mistake
of the first value of variable). At small sizes of a set mistake |∆1|
the sizes of speed of convergence at a variation |∆1| differ a
little on the size from each other. At the big sizes of a set mistake the speed
of convergence can differ from the speeds received at small sizes of a mistake |∆1|,
and it should be meant at the further calculations.
Then the technique of reception of recurrent formulas
for the solution UCE in focal points is.
Let suppose that k
= k0 + ∆k, where k0 is a focal point which can be equaled to any chosen
value from zero up to (+ ∞); ∆k
is a deviation from this focal point.
Let's substitute this expression in the formula (2)
and we solve the received equation relatively ∆k, considering that k0
is a constant quantity.


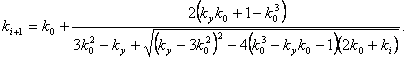 (6)
(6)
The
formula (6) represents the general recurrent formula for the solution UCE
At k0 = 0 from the formula (6)
we receive:
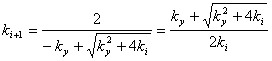 (7)
(7)
From the
second variant of the formula (7) we receive:
![]() (8)
(8)
Before
the sign √ in formulas (6), (7), (8) the sign «+» is taken after checking
of formulas in calculations.
At k0 = 1 from the formula (6) we receive
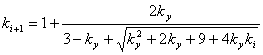 (9)
(9)
For the
orientation we calculate values ky
and k for RCE with double roots
![]()
Under the
formula (3) ![]()
From the formula (1) ![]() .
.
By the
technique which was given before we check up formulas (4), (5), (7), (8), (9) on
the convergence and the speed of convergence. The results of calculations
(characteristic points) are in Table 1.
The
analysis of Table 1 allows to draw the following conclusions.
The
formula (4) possesses convergence at ky > 0,61 , the speed of convergence of the formula
accrues with increase ky.
The
formula (5) possesses convergence at ky > 0,938 , the speed of convergence of the formula is
maximal in a narrow range at ky ≈ 0.
Formulas
(7), (8), (9) possess convergence at all possible values ky, but each formula possesses high speeds of
convergence in different areas of values ky, the formula (7) at ky
<< - 1, the formula (8) at ky >> 1, the formula
(9) at ky ≈ 0.
Table 1
|
k |
ky |
k1 |
The speeds
of convergence of the formula ¹ |
||||||||
|
4 |
5 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|||
|
0,01 |
-99,99 |
0,011 |
─ |
─ |
106 |
2,04 |
112,3 |
|
|
108 |
4∙1014 |
|
0,1 |
-9,99 |
0,11 |
─ |
─ |
103 |
2,05 |
11,3 |
|
|
104 |
4∙107 |
|
0,2 |
-4,96 |
0,21 |
─ |
─ |
126,0 |
2,04 |
6,9 |
|
|
869,4 |
4∙105 |
|
0,3 |
-3,24 |
0,31 |
─ |
─ |
38,1 |
2,07 |
7,7 |
|
|
293,3 |
4∙104 |
|
0,4 |
-2,34 |
0,41 |
─ |
─ |
16,6 |
2,11 |
6,7 |
|
|
112,7 |
8∙103 |
|
0,5 |
-1,75 |
0,51 |
─ |
─ |
9,0 |
2,26 |
8,9 |
|
|
80,4 |
4∙103 |
|
0,6 |
-1,306 |
0,61 |
─ |
─ |
5,6 |
2,44 |
13,8 |
|
|
77,2 |
2,5∙103 |
|
0,7 |
-0,938 |
0,71 |
─ |
1,58 |
3,94 |
2,7 |
35,6 |
|
|
140,2 |
4∙103 |
|
0,8 |
-0,61 |
0,81 |
1,01 |
3,16 |
2,97 |
3,0 |
62,1 |
|
995,6 |
184,4 |
4,9∙103 |
|
0,9 |
-0,3011 |
0,91 |
1,46 |
8,08 |
2,38 |
3,44 |
271,9 |
|
2∙105 |
647,1 |
1,8∙104 |
|
1,0 |
0 |
1,01 |
2,01 |
∞ |
2,01 |
4,01 |
∞ |
|
∞ |
∞ |
∞ |
|
1,1 |
0,3009 |
1,11 |
2,64 |
12,05 |
1,76 |
4,64 |
332,0 |
|
3∙106 |
584,3 |
2,2∙104 |
|
1,2 |
0,6066 |
1,21 |
3,48 |
7,12 |
1,59 |
5,47 |
91,9 |
1,7∙103 |
1,3∙105 |
148,1 |
6∙103 |
|
1,3 |
0,9207 |
1,31 |
4,36 |
5,51 |
1,46 |
6,37 |
45,16 |
6,8∙103 |
2,75∙104 |
65,9 |
3,9∙103 |
|
1,36 |
1,114 |
1,35 |
4,99 |
4,97 |
1,38 |
7,01 |
33,1 |
1,5∙104 |
1,5∙104 |
45,6 |
3∙103 |
|
1,5 |
1,583 |
1,51 |
6,79 |
4,26 |
1,3 |
8,76 |
19,6 |
9,7∙104 |
5,9∙103 |
|
2,5∙103 |
|
|
|
1,597 |
8,047 |
4,006 |
|
|
|
2,7∙105 |
4,1∙103 |
|
|
|
2 |
3,5 |
2,01 |
15,9 |
3,42 |
1,11 |
17,9 |
7,51 |
107 |
1,6∙103 |
|
2,9∙103 |
|
3 |
8,666 |
3,01 |
53,8 |
3,11 |
1,03 |
55,9 |
3,58 |
2∙1010 |
904,8 |
|
104 |
|
10,0 |
99,9 |
10,1 |
2019 |
3,01 |
1,01 |
2002 |
1,98 |
6∙1019 |
743,7 |
|
6∙106 |
It is
necessary to note, that in the field of the convergence it is possible to make
cascade formulas of recurrent formulas, i.e. to insert one or several formulas
into one another, and the speeds of convergence of cascade formulas are roughly
equal to the product of speeds of each formula included in it at identical
values of a parameter (ky).
For the
calculations in area ![]() (three material roots) from
formulas (4) and (8) it is possible to construct multicascade formulas, but
from the formula (4) multicascade formulas are more simple on structure.
(three material roots) from
formulas (4) and (8) it is possible to construct multicascade formulas, but
from the formula (4) multicascade formulas are more simple on structure.
Let
suppose that 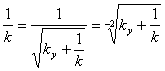 , then the
six-cascade formula on the basis of the formula (4) looks so:
, then the
six-cascade formula on the basis of the formula (4) looks so:
 (10)
(10)
The
formula (10) is applicable thanks to the high speeds of convergence at ky > 0,6. Formulas (5) and
(9) also allow to build cascade formulas with the high speeds at ky ≈ 0, but the formula
(5) is more preferable, for example, the six-cascade formula is below submitted
on the basis of the formula (5)
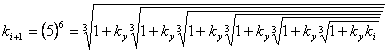 (11)
(11)
In a range
ky < 0 the application
of cascade formulas is possible on the basis of formulas (7) and (9).
Let's
substitute in (9) formula (7), we receive:
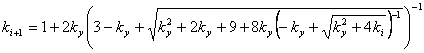 (12)
(12)
Taking
into account the convergence of formulas (7), (8), (9) at all possible values ky, it is possible to unite
these formulas in various combinations and to receive universal recurrent
formulas for the solution UCE 1. The formula is below constructed on a
pattern (7) ∙ (8) ∙ (9).
 (13)
(13)
The speeds of convergence of formulas (10), (11), (12), (13) are in
Table 1. As the first (initial) value ki = k1 in recurrent formulas UCE 1 it is
possible to substitute number k1
= 1 or the number which has been picked up on the value ky from
Table 1.
4. Formula UCE2.
Let ![]() (1)
(1)
After
the substitution (1) in formula RCE (1 6) and transformations we receive the
formula of the universal cubic equation of kind 2 (for brevity: UCE-2)
![]() (2)
(2)
where  . (3)
. (3)
At B < 0 the equation
(2) becomes:
![]() (4)
(4)
m = 1 ÷ (+ ∞), my = 0 ÷ (+ ∞).
At B > 0 we have:
![]() (5)
(5)
m = 0 ÷ (- ∞), my = 0 ÷ (- ∞).
Let's
calculate the sizes my and m for RCE with double roots, and also for RCE,
at which maximal and minimal (on the module) sizes of roots differ, for
example, in 1000 times.
![]()
Under
formula (3) ![]()
From
formula (1) 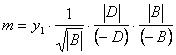 (6)
(6)
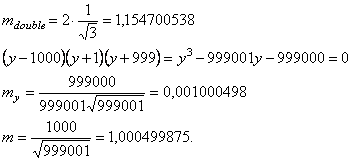
From
the examples it is visible, that the area of values my, at which all 3 roots RCE have
material sizes, is between 0 and ![]() and the size m is in area with borders 1 and
and the size m is in area with borders 1 and ![]()
The
following most productive recurrent formulas have been received and selected
from the formula (4), also after using of the substitution![]() :
:
![]() (7)
(7)
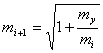 (8)
(8)
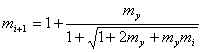 (9)
(9)
The
results of calculations for the speed of convergence of the received recurrent
formulas with the use of a technique of unit (3) are collected in Table 2.
Table
2.
|
m |
my |
m1 |
The
speeds of convergence of the formula ¹ |
||||
|
7 |
8 |
9 |
10 |
11 |
|||
|
1 |
0 |
1,01 |
3,0 |
∞ |
∞ |
729 |
∞ |
|
1,05 |
0,1076 |
1,051 |
3,3 |
21,5 |
922,0 |
1291 |
7,8∙108 |
|
1,1 |
0,231 |
1,11 |
3,63 |
11,6 |
262,1 |
2,2∙103 |
1,8∙107 |
|
1,15 |
0,3708 |
1,16 |
3,97 |
8,26 |
131,0 |
3,9∙103 |
2,2∙106 |
|
1,1547 |
0,384900179 |
1,1447 |
|
|
124,23 |
|
1,917∙106 |
|
1,155 |
0,38579 |
1,154 |
4,001 |
7,981 |
123,9 |
4,1∙103 |
1,9∙106 |
|
1,2 |
0,528 |
1,21 |
4,32 |
6,59 |
82,0 |
6,4∙103 |
|
|
1,5 |
1,875 |
1,51 |
6,75 |
3,62 |
22,0 |
9,4∙104 |
|
|
2 |
6,0 |
2,01 |
12,0 |
2,67 |
10,0 |
2,98∙106 |
|
|
3 |
24,0 |
3,01 |
27,0 |
2,25 |
5,5 |
3,8∙108 |
|
|
10 |
990 |
10,1 |
300,0 |
2,03 |
2,7 |
7∙1014 |
|
|
100 |
999900 |
100,1 |
3∙104 |
2,0 |
2,06 |
7∙1026 |
|
After the analysis of Table 2 it is possible to draw
the following conclusions.
All three formulas possess convergence at my
> 0.
The
formula (7) increases the speed of convergence at increase my. Formulas (8) and (9) possess a
maximum of the speed at my
→ 0. The formula
(9) possesses at small my considerably the big speeds, than the formula (8).
All three formulas allow to build multicascade
formulas. For example, we receive the six-cascade formula on the basis of the
formula (7):
 (10)
(10)
On
the basis of the formula (9) it is possible to construct two, three,
four-cascade formulas with the speeds of convergence at my
=
0,38579.
V2 = 1,5∙104; V3 = 1,9∙106; V4 = 2,3∙108
The
three-cascade formula is below resulted on the basis of the formula (9):
 (11)
(11)
The
speeds of convergence of formulas (10), (11) are resulted in Table 2. The first
(initial) value mi = m1 äëÿ ôîðìóë (7) ÷ (11) is possible to take number
m1 = 1.
For
UCE 2 at B > 0, my < 0 from the formula (5) it is possible
to receive the following most productive recurrent formulas:
![]() (12)
(12)
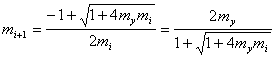 (13)
(13)
Having substituted in the formula (5) expressions |m| = 1 + |∆m| è |m| = 0,5 + |∆m|, we
receive:
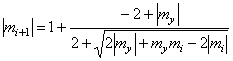 (14)
(14)
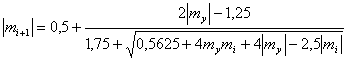 (15)
(15)
The
speed of convergence of formulas (12), (13), (14), (15) are in Table 3.
After
the analysis of Table 3 it is possible to draw the following conclusions.
The
formula (12) possesses convergence at my < - 0,816, the speed of
convergence of the formula grows with increase in the module |my|.
The
formula (13) possesses convergence at my < 0, a maximum of speed at |my|→0.
The
formula (14) possesses a maximum of speed at my = 2,0 , and
on both sides from the value my = 2,0 speeds fall.
The
formula (15) possesses a maximum of speed at my = 0,625, and on both sides from the
value my = 0,625 speeds
fall.
Table 3.
|
- m |
- my |
- m1 |
12 |
13 |
14 |
15 |
16 |
17 |
|
0,1 |
0,101 |
0,11 |
─ |
102,1 |
─ |
5,37 |
|
104 |
|
0,2 |
0,208 |
0,21 |
─ |
27,09 |
─ |
11,3 |
|
733,8 |
|
0,3 |
0,327 |
0,31 |
─ |
13,17 |
1,53 |
30,6 |
|
173,4 |
|
0,4 |
0,464 |
0,41 |
─ |
8,29 |
3,05 |
146,7 |
|
68,7 |
|
0,5 |
0,625 |
0,51 |
─ |
6,03 |
5,94 |
∞ |
|
36,3 |
|
0,6 |
0,816 |
0,61 |
1,06 |
4,8 |
11,9 |
207,1 |
|
23,0 |
|
0,7 |
1,043 |
0,71 |
1,45 |
4,06 |
26,3 |
60,8 |
|
16,4 |
|
0,8 |
1,312 |
0,81 |
1,9 |
3,58 |
71,8 |
31,5 |
|
12,8 |
|
0,9 |
1,629 |
0,91 |
2,4 |
3,25 |
341,7 |
20,98 |
|
10,5 |
|
1,0 |
2,0 |
1,01 |
2,98 |
3,01 |
∞ |
15,03 |
78,8 |
9,06 |
|
1,1 |
2,431 |
1,11 |
3,62 |
|
462,1 |
|
171,7 |
|
|
1,2 |
2,928 |
1,21 |
4,31 |
2,7 |
132,0 |
|
345,0 |
|
|
1,3 |
3,497 |
1,31 |
5,06 |
|
66,5 |
|
655,5 |
|
|
1,5 |
4,875 |
1,51 |
6,74 |
2,45 |
30,0 |
|
2∙103 |
|
|
2,0 |
10 |
2,01 |
11,99 |
2,25 |
12,01 |
|
2∙104 |
|
|
10,0 |
1010 |
10,1 |
29,9 |
2,02 |
2,73 |
|
8∙105 |
|
On
the basis of the formula (12) it is possible to build multicascade formulas
with high speeds of convergence. For example the four-cascade formula (16) is
below.
![]() (16)
(16)
On
the basis of the formula (13) it is also possible to construct two, three, four
-cascade formulas. For example the two-cascade formula (17) is below.
 (17)
(17)
The
speeds of convergence of formulas (16), (17) are in Table 3. The initial values
mi
= m1 for formulas (12) ÷ (17) can be taken m1 = 1.
The
fields of application of formulas can be chosen according Table 3 depending on
the speed of convergence of the concrete formula.
5. Formulas UCE 3 and UCE n.
Let ![]() (1)
(1)
Having
substituted (1) in formula RCE (1 6), we receive formula UCE 3:
![]() (2)
(2)
where ![]() (3)
(3)
If
we use the formula
![]() (4)
(4)
we receive formula UCE n:
![]() (5)
(5)
Between
formulas (2) and (5) there is a connection as
![]() (6)
(6)
Accordingly,
formulas (1) and (4) can be written down as:
![]() (7)
(7)
It
is possible later on to transform all formulas received for the solution UCE with
use of formulas (6).
Let's
calculate sizes ty, t and n for RCE with double roots:
![]()
Under formula (3) ![]()
From formula (1) ![]()
From formula (4) ![]()
From
formulas (2) and (5) it is possible to receive the following most effective
recurrent formulas:
![]() (8)
(8)
 (9)
(9)
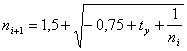 (10)
(10)
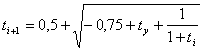 (11)
(11)
Having
made substitutions t = 1 + ∆t and t = 0,5
+ ∆t in the formula (2), after
transformations we receive recurrent formulas for solution UCE
 (12)
(12)
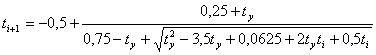 (13)
(13)
In
table 4 the results of calculations are shown for the speed of convergence by a
technique of unit 3 of recurrent formulas (8), (12), (13).
Table 4.
|
t |
ty |
t1 |
The
speeds of convergence of the formula ¹ |
||||||
|
8 |
12 |
13 |
14 |
15 |
|
|
|||
|
-0,9 |
-7,29 |
-0,91 |
─ |
970,7 |
59,7 |
9∙105 |
|
|
|
|
-0,8 |
-2,56 |
-0,81 |
─ |
110,8 |
48,8 |
104 |
|
|
|
|
-0,75 |
-1,687 |
-0,76 |
─ |
52,9 |
53,0 |
2,7∙103 |
|
|
|
|
-0,7 |
-1,143 |
-0,71 |
─ |
27,9 |
64,4 |
781,2 |
|
|
|
|
-0,6 |
-0,54 |
-0,61 |
1,98 |
9,05 |
161,1 |
82,0 |
15,4 |
|
|
|
-0,55 |
-0,369 |
-0,56 |
2,43 |
5,238 |
510,27 |
27,4 |
35,2 |
|
|
|
-0,5 |
-0,25 |
-0,51 |
2,97 |
2,92 |
∞ |
8,5 |
78,7 |
|
|
|
-0,4 |
-0,106 |
-0,41 |
4,47 |
─ |
57,4 |
|
400,9 |
|
|
|
-0,3 |
-0,038 |
-0,31 |
6,96 |
─ |
6,56 |
|
2,3∙103 |
|
|
|
-0,2 |
-0,01 |
-0,21 |
11,94 |
─ |
─ |
|
2∙104 |
|
|
|
-0,1 |
-0,00111 |
-0,11 |
26,8 |
─ |
─ |
|
5∙105 |
|
|
|
0 |
0 |
0,01 |
∞ |
|
|
|
∞ |
|
|
The continuation of Table 4.
|
t |
ty |
t1 |
8 |
9 |
11 |
16 |
15 |
18 |
17 |
|
0,1 |
0,000909 |
0,11 |
33,09 |
─ |
─ |
|
106 |
|
|
|
0,2 |
0,0066 |
0,21 |
18,04 |
2,49 |
─ |
|
105 |
|
|
|
0,5 |
0,0833 |
0,51 |
9,01 |
3,049 |
─ |
86,4 |
0,6∙103 |
|
803,4 |
|
1,0 |
0,5 |
1,01 |
6,0 |
4,034 |
4,0 |
264,8 |
1,3∙103 |
|
4,3∙103 |
|
2,0 |
2,666 |
2,01 |
4,5 |
6,027 |
27 |
1319,4 |
411,8 |
729,0 |
4,7∙104 |
|
3,0 |
6,75 |
3,01 |
4,0 |
8,02 |
80,1 |
4∙103 |
256,0 |
6,4∙103 |
2,6∙105 |
|
5,0 |
20,88 |
5,01 |
3,6 |
12,0 |
324,5 |
2∙104 |
167,0 |
105 |
2,9∙106 |
|
10,0 |
90,909 |
10,1 |
3,31 |
22,2 |
2319,8 |
2,4∙105 |
120,0 |
5∙106 |
1,1∙108 |
After
the analysis of Table 4 it is possible to draw the following conclusions.
The
formula (8) possesses a maximum of speed of convergence at ty = 0, the working area of values of a
parameter ty ≥ 0,25.
The
formula (9) possesses convergence at ty > 0, with increase in the size ty the speed grows.
The
formula (11) possesses convergence at ty ≥ 0,5, the speed of
convergence of the formula quickly increases with growth ty.
The
formula (12) possesses convergence at ty ≤ 0,25, the speed of
the formula quickly increases at ty → ∞.
The
formula (13) possesses a maximum of speed at ty = 0,25, the working area of a
parameter ty from (
∞) to( 0,1066).
On the basis of formulas (8), (9), (11), (12) it is
possible to receive cascade formulas.
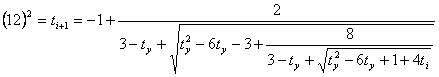 (14)
(14)
![]() (15)
(15)
From
formula (9) we get
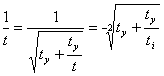
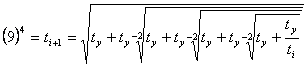 (16)
(16)
 (17)
(17)
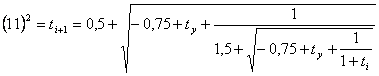 (18)
(18)
The
speeds of convergence of formulas (14)
÷ (18) are shown above in Table 4. The working values ty and rough-approached values ti
= t1 for the
received formulas are possible to take from Table 4 proceeding from the value ty and sizes of the speed of convergence
of the given formula.
5.1
Formula
UCE n+.
At n < 1,
ty < 0 the
equation (5 5) is more convenient for solving at the replacement of a
variable «n» on other variable
![]() or
or ![]() (1)
(1)
After
the substitution (1) in (5 5) we receive the formula UCE n+:
![]() .
(2)
.
(2)
After
the transformations from the formula (2) it is possible to receive the
following most effective recurrent formulas:
![]()
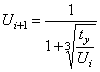 (3)
(3)
![]()
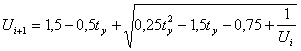 (4)
(4)
After
the substitution U = 2 + ∆U in the formula (2) it is
possible to receive:
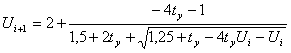 (5)
(5)
The
results of calculations for the speed of convergence of formulas (3), (4), (5)
are in Table 5 by a technique of unit 3.
After
the analysis of Table 5 it is possible to draw the following conclusions.
The
formula (3) possesses the high speed of convergence at ty → 0 , the speed decreases with reduction ty (increase in the module |ty|).
The
formula (4) possesses the speed of convergence more than 3 at ty ≤ 0,25 , and if the module |ty| is
more, then the speed of convergence is more too.
The
formula (5) possesses a maximum of speed at ty ≈ 0,25 , and on both
sides from this point the speeds fall.
Table 5.
|
U |
ty |
U1 |
The
speeds of convergence of the formula ¹ |
|||||
|
3 |
5 |
4 |
6 |
7 |
8 |
|||
|
1 |
0 |
1,01 |
∞ |
─ |
─ |
∞ |
|
|
|
1,1 |
-0,00082 |
1,11 |
30,19 |
─ |
─ |
8,3∙105 |
|
|
|
1,3 |
-0,0159 |
1,31 |
10,05 |
─ |
─ |
104 |
|
|
|
1,5 |
-0,0555 |
1,51 |
6,033 |
─ |
─ |
1,3∙103 |
|
|
|
1,7 |
-0,1186 |
1,71 |
4,308 |
10,75 |
─ |
344,4 |
115,5 |
|
|
1,75 |
-0,1377 |
1,76 |
4,02 |
18,18 |
─ |
261,4 |
330,6 |
|
|
1,8 |
-0,158 |
1,81 |
3,769 |
32,6 |
─ |
200,5 |
1066,4 |
|
|
1,9 |
-0,2019 |
1,91 |
3,35 |
165,04 |
─ |
125,9 |
2,7∙104 |
|
|
2,0 |
-0,25 |
2,01 |
3,014 |
∞ |
3,001 |
82,5 |
∞ |
|
|
2,1 |
-0,3018 |
2,11 |
2,74 |
235,4 |
3,968 |
|
5,5∙104 |
|
|
2,3 |
-0,415 |
2,31 |
─ |
34,16 |
6,285 |
|
1,1∙103 |
|
|
2,5 |
-0,54 |
2,51 |
─ |
15,23 |
9,154 |
|
231,9 |
83,7 |
|
2,6 |
-0,6059 |
2,61 |
─ |
11,6 |
10,81 |
|
134,7 |
116,8 |
|
2,7 |
-0,6739 |
2,71 |
─ |
9,288 |
12,62 |
|
86,2 |
159,3 |
|
3,0 |
-0,8888 |
3,01 |
─ |
─ |
19,058 |
|
|
383,3 |
|
5,0 |
-2,56 |
5,01 |
─ |
─ |
111,2 |
|
|
1,2∙104 |
|
10,0 |
-7,29 |
10,1 |
─ |
─ |
980,6 |
|
|
9,6∙105 |
On
the basis of formulas (3), (5), (4) it is possible to construct cascade
formulas with the increased speeds of convergence.
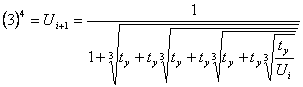 (6)
(6)
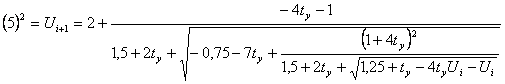 (7)
(7)
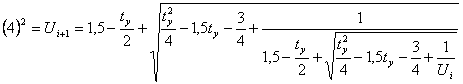 (8)
(8)
The
speeds of convergence of formulas (6), (7), (8) are shown in Table 5. It is possible
to take the initial values Ui = U1 for formulas (3) and (6) U1 = 1, for formulas (5) and (7) U1 = 2, for formulas (4) and (8) U1 = 3, or the proper value ty according Table 5.
5.2
The
formula UCE 3 +.
Let's
replace in the formula (5 2) a variable t
on the other variable d with the
substitution ![]() (1)
(1)

Let's
designate 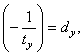 then (2)
then (2)
![]() (3)
(3)
The
received formula (3) we name the formula UCE 3 +.
At
the change t in a range from 0 up to
1 the size d
varies from + ∞ up to + 1, the size dy from + ∞ to 0.
From
the formula (3) with the using of substitutions
![]()
we receive the formulas for the solution
UCE 3 + in a vicinity of points d0 = 1 è d0 = 2.
 (4)
(4)
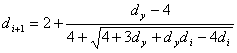 (5)
(5)
From
the formula (5 8) with the use of formulas (1) and (2) we receive 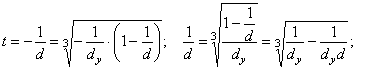
 .
(6)
.
(6)
The
speeds of convergence of the formulas (4), (5), (6) designed by a technique of
Unit 3. They are in Table 6.
The
analysis of Table 6 allows to draw the following conclusions.
The
formula (4) possesses a maximum of the speed of convergence at dy → 0, and at increase dy speed falls.
The
formula (5) possesses a maximum of the speed at dy ≈ 4 and on both sides from a point
dy =4 speeds fall.
The
formula (6) possesses convergence at dy > 0,784 and the speed grows with increase dy.
Table 6.
|
d |
dy |
d1 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
0 |
1,01 |
∞ |
─ |
─ |
∞ |
|
|
|
1,1 |
0,121 |
1,11 |
142,1 |
─ |
─ |
2,8∙106 |
|
|
|
1,3 |
0,507 |
1,31 |
26,5 |
─ |
─ |
1,8∙104 |
|
|
|
1,4 |
0,784 |
1,41 |
18,2 |
7,5 |
1,22 |
6∙103 |
|
|
|
1,5 |
1,125 |
1,51 |
14,0 |
13,9 |
1,5 |
2,7∙103 |
194,3 |
|
|
1,6 |
1,536 |
1,61 |
11,4 |
26,9 |
1,82 |
1,4∙103 |
725,7 |
|
|
1,8 |
2,592 |
1,81 |
8,58 |
51,8 |
2,4 |
631,6 |
2,3∙104 |
|
|
1,9 |
3,249 |
1,91 |
7,69 |
701,7 |
2,7 |
454,7 |
4,9∙105 |
|
|
2,0 |
4,0 |
2,01 |
7,01 |
∞ |
3,02 |
344,4 |
∞ |
83,7 |
|
2,1 |
4,851 |
2,11 |
6,47 |
902,1 |
3,32 |
270,8 |
8∙105 |
122,2 |
|
2,3 |
6,87 |
2,31 |
5,68 |
124,2 |
3,92 |
183,2 |
1,5∙104 |
237,3 |
|
2,5 |
9,375 |
2,51 |
5,12 |
54,0 |
4,52 |
|
2,9∙103 |
419,5 |
|
2,7 |
12,3 |
2,71 |
|
32,6 |
5,12 |
|
103 |
690,5 |
|
2,8 |
14,1 |
2,81 |
|
27,0 |
5,42 |
|
730,1 |
867,0 |
|
3,0 |
18,0 |
3,01 |
|
20,0 |
6,02 |
|
400 |
1319,1 |
|
5,0 |
100,0 |
5,01 |
|
|
12,0 |
|
|
2∙104 |
|
10,0 |
900 |
10,1 |
|
|
27,2 |
|
|
5,5∙105 |
On
the basis of formulas (4), (5), (6) it is possible to build cascade formulas
with the increased speeds of convergence.
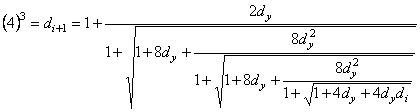 (7)
(7)
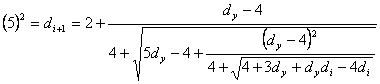 (8)
(8)
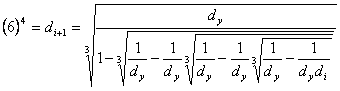 (9)
(9)
The
speeds of convergence of formulas (7), (8), (9) are collected in Table 6. As the
first initial value di = d1 in formulas (4) ÷ (9) it is possible to substitute number
d1 = 2.
6. The transformation of formulas UCE.
As all
UCE are derivatives from RCE it is possible to transform formulas of the solution
of one kind of UCE to the formulas of the solution of other kinds RCE.
First of all the formulas
with the big speeds of convergence are interesting for the solution UCE in the
area where there are three material roots (i.e. areas ty ≥ 6,75).
At the
comparison of such formulas the formulas (4 9) and (5 11) for the solution
UCE 2 and UCE 3 are suitable.
Taking
into account, that in the field of three material roots there are factors ky,
my and ty > 0, also there are variables k, m, t, which are more than 0 we establish
connections between the factors and the variables of the different UCE in these
conditions.
![]()
![]() (1)
(1)
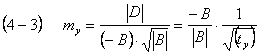
At my > 0 B < 0, therefore
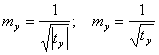 (2)
(2)
![]()
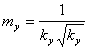 (3)
(3)
![]()
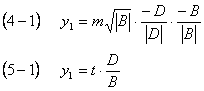
Equating
to each other mentioned formulas above, we receive:
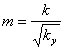 (4)
(4)
![]() (5)
(5)
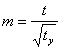 (6)
(6)
Let's
write out the formula (4 9) for the solution UCE 2
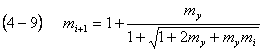
Let's
transform the formula (4 9), having substituted in it formulas (4) and (3):
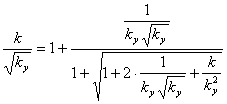
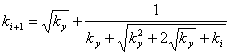 (7)
(7)
Let's
transform the formula (4 9), having substituted in it formulas (2) and (6)
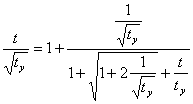
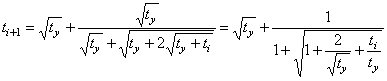 (8)
(8)
Let's
write out the formula (5 11) for the solution UCE 3
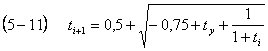
Let's
transform the formula (5 11), having substituted in it formulas (1) and (5)
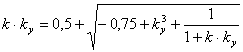
 (9)
(9)
On
the basis of formulas (7), (9), (8) we construct three-cascade recurrent
formulas with the increased speeds of convergence:
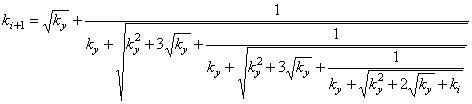 (10)
(10)
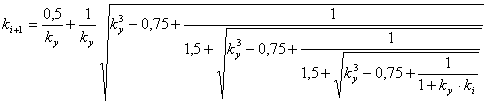 (11)
(11)
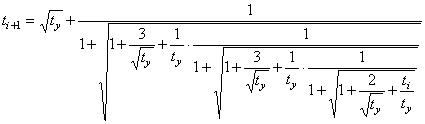 (12)
(12)
Let's
consider, how the size of a mistake of result varies at the substitution of the
different values ti = t1 in formulas (5 9) and (5 11).
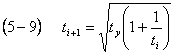
For
example we take the value t = 3 and ty = 6,75.
If ti = t1 = ∞,
then ![]() (13)
(13)
![]() , error
, error ![]()
If ![]() , then
, then 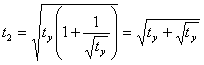 (14)
(14)
![]()
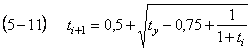
At t1 = ∞ ![]()
At t1 = 1 ![]()
At ![]()
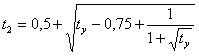 (15)
(15)
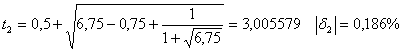
The
calculations under the formula (8) at ![]() give us:
give us:
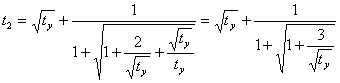 (16)
(16)
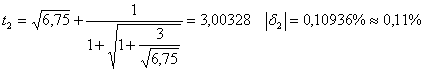
The
similar calculations for UCE 1 and UCE 2 give the following formulas:
From formula (3 4) ![]() (17)
(17)
From formula (7) 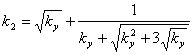 (18)
(18)
From formula (4 9) for ÓÊÓ 2 at m =
1
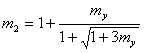 (19)
(19)
Contents
|
Introduction
... |
1 |
|
1. The using of formula Cardano
... |
2 |
|
2. The
calculation of the second and third roots of the cubic equation
. |
3 |
|
3. The universal cubic equation of kind 1
.. |
4 |
|
4. Formula UCE 2
... |
11 |
|
5. Formulas UCE 3 and UCE n
... |
16 |
|
5.1.
Formula UCE n +
.. |
19 |
|
5.2.
The formula UCE 3 +
... |
21 |
|
6. The transformation of formulas
UCE
......................... |
24 |
Hairetdinov
Robert Farrahovich
THE SOLUTION OF THE CUBIC
EQUATIONS.
Literature:
1.
I.N.Bronstein,
K.A.Semendjaev, The Reference book on Mathematics, edition 5,
2.
R.F.Hairetdinov, The Solution of the
Cubic Equations, edition 2,
Translator Sharafutdinova
Elena Sergeevna.